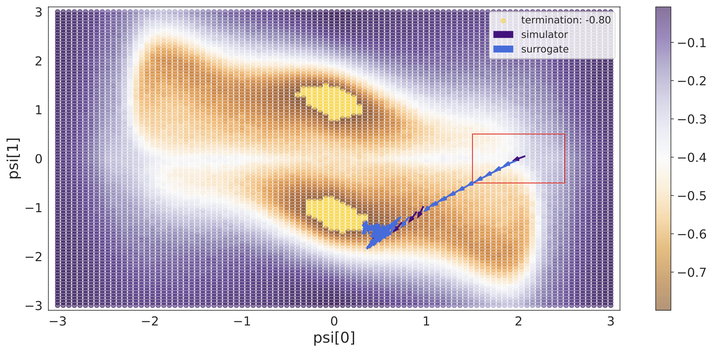
 Optimising the ThreeHump problem.
Optimising the ThreeHump problem.Abstract
In recent years, solving inverse problems for black-box simulators has become a point of focus for the machine learning community due to their ubiquity in science and engineering scenarios. In such settings, the simulator describes a forward process from simulator parameters \psi and input data x to observations y, and the goal of the inverse problem is to optimise \psi to minimise some observation loss. Simulator gradients are often unavailable or prohibitively expensive to obtain, making optimisation of these simulators particularly challenging. Moreover, in many applications, the goal is to solve a family of related inverse problems. Thus, starting optimisation ab-initio/from-scratch may be infeasible if the forward model is expensive to evaluate. In this paper, we propose a novel method for solving classes of similar inverse problems. We learn an active learning policy that guides the training of a surrogate and use the gradients of this surrogate to optimise the simulator parameters with gradient descent. After training the policy, downstream inverse problem optimisations require up to 90% fewer forward model evaluations than the baseline.